Приветствую всех, тема довольно сложна для понимания, и требует вашей концентрации внимания.
АВЛ-дерево – сбалансированное по высоте двоичное дерево поиска. Было названо в честь советских учёных Адельсона-Вельского Георгия Максимовича и Ландиса Евгения Михайловича, которые впервые описали алгоритм и его структуру. Правила построения двоичных деревьев поиска:
- каждый узел может иметь не более двух потомков (левый и правый);
- значения которые меньше текущего размещаются в левом поддереве;
- значения которые больше или равные текущему размещаются в правом поддереве;
Дополнительное условие для АВЛ-дерева:
- для любого узла дерева, высота его правого поддерева никогда не превышает высоты его
левого поддерева более чем на единицу.
*Этого свойства достаточно, чтобы высота дерева имела логарифмическую зависимость от
числа его узлов.
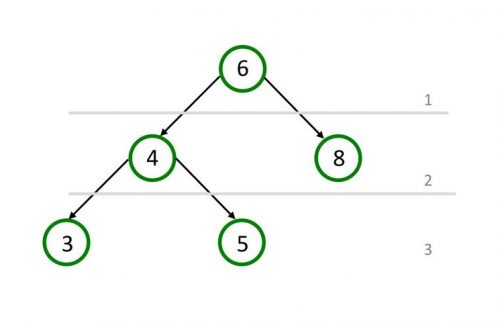
Узел «6» не имеет родительского узла, поэтому он является корнем дерева и находится на первом уровне. Узлы «4» и «8» это братские узлы, которые находятся на втором уровне. Узлы «3» и «5» находятся на третьем уровне. Используя эти уровни, можно найти расстояние между узлами «6» и «3», оно равно двум.
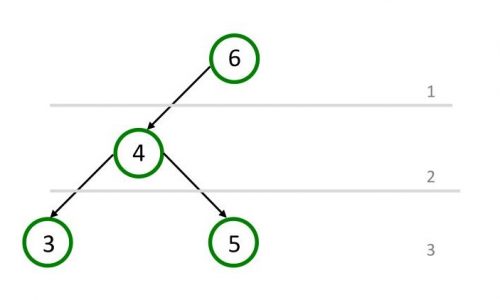
Не сбалансированное дерево
Минимальная высота левого и правого поддерева не может отличатся больше чем на единицу и это правило характерно для всех узлов дерева. Если рассмотреть корень узла, то его левое поддерево имеет высоту два, а правое – ноль, поэтому дерево не сбалансировано.
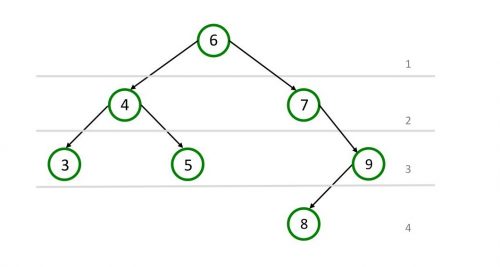
Частично сбалансированное дерево
Дерево называется полностью сбалансированным, если каждый узел дерева сбалансированный. Узел «7» не сбалансированный, поскольку высота правого поддерева два, а левого – ноль.
Алгоритм балансировки
Для определения сбалансировано дерево по высоте или нет, требуется проверить высоту правого и левого потомка каждого узла. При необходимости балансировки, узлы подлежат удалению, добавлению или вращению.
АВЛ-деревья используют базовые алгоритмы вращения узла:
- правое вращение,
- левое вращение,
- два смешанных алгоритма, которые базируются на первых двух.
Существуют четыре типа вращения:
- вращение влево,
- вращение вправо,
- вращение влево,
- а потом в право и в обратной последовательности.
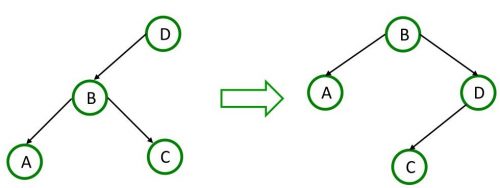
Вращение узла вправо
Алгоритм вращения вправо имеет три шага:
- земенить текущий корень на его левого потомка; узел B становится корнем, а узел А занимает его место.
- переместить правого потомка нового корня на место левого потомка старого корня. B -> C to D -> C.
- Присвоить новому корню (B) в качестве правого потомка старый корень (D).
Вращение узла влево
Алгоритм вращения влево осуществляется в три шага:
- земенить текущий корень на его правого потомка; узел «С» становится корнем, а узел «А» его левым потомком.
- переместить левого потомка нового корня (B) на место правого потомка старого корня. «С» -> «B» to «A» -> «B».
- Присвоить новому корню (С) в качестве правого узла значение старого корня (D).
Вращение вправо и влево
Данная ситуация отличается от предыдущих, поскольку правый потомок корня имеет левого потомка, но не имеет правого.
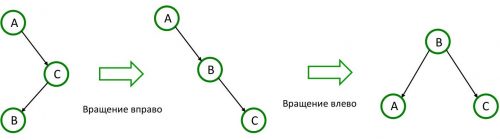
Вращение влево и вправо
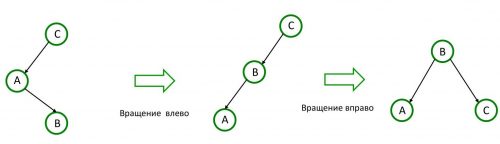
Когда корень дерева имеет левого потомка, который в свою очередь имеет правого потомка, но не имеет левого, применяют последовательной вращения влево, а затем вправо.
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
namespace AVLTreeNode
{
// Класс AVLTreeNode реализует один узел АВЛ дерева
public class AVLTreeNode<TNode> : IComparable<TNode> where TNode : IComparable
{
AVLTree<TNode> _tree;
AVLTreeNode<TNode> _left; // левый потомок
AVLTreeNode<TNode> _right; // правый потомок
#region Конструктор
public AVLTreeNode(TNode value, AVLTreeNode<TNode> parent, AVLTree<TNode> tree)
{
Value = value;
Parent = parent;
_tree = tree;
}
#endregion
#region Свойства
public AVLTreeNode<TNode> Left
{
get
{
return _left;
}
internal set
{
_left = value;
if (_left != null)
{
_left.Parent = this; // установка указателя на родительский элемент
}
}
}
public AVLTreeNode<TNode> Right
{
get
{
return _right;
}
internal set
{
_right = value;
if (_right != null)
{
_right.Parent = this; // установка указателя на родительский элемент
}
}
}
// Указатель на родительский узел
public AVLTreeNode<TNode> Parent
{
get;
internal set;
}
// значение текущего узла
public TNode Value
{
get;
private set;
}
// Сравнивает текущий узел по указаному значению, возвращет 1, если значение экземпляра больше переданного значения,
// возвращает -1, когда значение экземпляра меньше переданого значения, 0 - когда они равны.
#endregion
#region CompareTo
public int CompareTo(TNode other)
{
return Value.CompareTo(other);
}
#endregion
#region Balance
internal void Balance()
{
if (State == TreeState.RightHeavy)
{
if (Right != null && Right.BalanceFactor < 0)
{
LeftRightRotation();
}
else
{
LeftRotation();
}
}
else if (State == TreeState.LeftHeavy)
{
if (Left != null && Left.BalanceFactor > 0)
{
RightLeftRotation();
}
else
{
RightRotation();
}
}
}
private int MaxChildHeight(AVLTreeNode<TNode> node)
{
if (node != null)
{
return 1 + Math.Max(MaxChildHeight(node.Left), MaxChildHeight(node.Right));
}
return 0;
}
private int LeftHeight
{
get
{
return MaxChildHeight(Left);
}
}
private int RightHeight
{
get
{
return MaxChildHeight(Right);
}
}
private TreeState State
{
get
{
if (LeftHeight - RightHeight > 1)
{
return TreeState.LeftHeavy;
}
if (RightHeight - LeftHeight > 1)
{
return TreeState.RightHeavy;
}
return TreeState.Balanced;
}
}
private int BalanceFactor
{
get
{
return RightHeight - LeftHeight;
}
}
enum TreeState
{
Balanced,
LeftHeavy,
RightHeavy,
}
#endregion
#region LeftRotation
private void LeftRotation()
{
// До
// 12(this)
// \
// 15
// \
// 25
//
// После
// 15
// / \
// 12 25
// Сделать правого потомка новым корнем дерева.
AVLTreeNode<TNode> newRoot = Right;
ReplaceRoot(newRoot);
// Поставить на место правого потомка - левого потомка нового корня.
Right = newRoot.Left;
// Сделать текущий узел - левым потомком нового корня.
newRoot.Left = this;
}
#endregion
#region RightRotation
private void RightRotation()
{
// Было
// c (this)
// /
// b
// /
// a
//
// Стало
// b
// / \
// a c
// Левый узел текущего элемента становится новым корнем
AVLTreeNode<TNode> newRoot = Left;
ReplaceRoot(newRoot);
// Перемещение правого потомка нового корня на место левого потомка старого корня
Left = newRoot.Right;
// Правым потомком нового корня, становится старый корень.
newRoot.Right = this;
}
#endregion
#region LeftRightRotation
private void LeftRightRotation()
{
Right.RightRotation();
LeftRotation();
}
#endregion
#region RightLeftRotation
private void RightLeftRotation()
{
Left.LeftRotation();
RightRotation();
}
#endregion
#region Перемещение корня
private void ReplaceRoot(AVLTreeNode<TNode> newRoot)
{
if (this.Parent != null)
{
if (this.Parent.Left == this)
{
this.Parent.Left = newRoot;
}
else if (this.Parent.Right == this)
{
this.Parent.Right = newRoot;
}
}
else
{
_tree.Head = newRoot;
}
newRoot.Parent = this.Parent;
this.Parent = newRoot;
}
#endregion
}
}
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
namespace AVLTreeNode
{
public class AVLTree<T> : IEnumerable<T> where T : IComparable
{
// Свойство для корня дерева
public AVLTreeNode<T> Head
{
get;
internal set;
}
#region Количество узлов дерева
public int Count
{
get;
private set;
}
#endregion
#region Метод Add
// Метод добавлет новый узел
public void Add(T value)
{
// Вариант 1: Дерево пустое - создание корня дерева
if (Head == null)
{
Head = new AVLTreeNode<T>(value, null, this);
}
// Вариант 2: Дерево не пустое - найти место для добавление нового узла.
else
{
AddTo(Head, value);
}
Count++;
}
// Алгоритм рекурсивного добавления нового узла в дерево.
private void AddTo(AVLTreeNode<T> node, T value)
{
// Вариант 1: Добавление нового узла в дерево. Значение добавлемого узла меньше чем значение текущего узла.
if (value.CompareTo(node.Value) < 0)
{
//Создание левого узла, если его нет.
if (node.Left == null)
{
node.Left = new AVLTreeNode<T>(value, node, this);
}
else
{
// Переходим к следующему левому узлу
AddTo(node.Left, value);
}
}
// Вариант 2: Добавлемое значение больше или равно текущему значению.
else
{
//Создание правого узла, если его нет.
if (node.Right == null)
{
node.Right = new AVLTreeNode<T>(value, node, this);
}
else
{
// Переход к следующему правому узлу.
AddTo(node.Right, value);
}
}
//node.Balance();
}
#endregion
#region Метод Contains
public bool Contains(T value)
{
return Find(value) != null;
}
/// <summary>
/// Находит и возвращает первый узел который содержит искомое значение.
/// Если значение не найдено, возвращает null.
/// Так же возвращает родительский узел.
/// </summary> ///
/// <param name="value">Значение поиска</param>
/// <param name="parent">Родительский элемент для найденного значения/// </param>
/// <returns> Найденный узел (или ноль) /// </returns>
private AVLTreeNode<T> Find(T value)
{
AVLTreeNode<T> current = Head; // помещаем текущий элемент в корень дерева
// Пока текщий узел на пустой
while (current != null)
{
int result = current.CompareTo(value); // сравнение значения текущего элемента с искомым значением
if (result > 0)
{
// Если значение меньшне текущего - переход влево
current = current.Left;
}
else if (result < 0)
{
// Если значение больше текщего - переход вправо
current = current.Right;
}
else
{
// Элемент найден
break;
}
}
return current;
}
#endregion
#region Метод Remove
public bool Remove(T value)
{
AVLTreeNode<T> current;
current = Find(value); // находим узел с удаляемым значением
if (current == null) // узел не найден
{
return false;
}
AVLTreeNode<T> treeToBalance = current.Parent; // баланс дерева относительно узла родителя
Count--; // уменьшение колиества узлов
// Вариант 1: Если удаляемый узел не имеет правого потомка
if (current.Right == null) // если нет правого потомка
{
if (current.Parent == null) // удаляемый узел является корнем
{
Head = current.Left; // на место корня перемещаем левого потомка
if (Head != null)
{
Head.Parent = null; // убераем ссылку на родителя
}
}
else // удаляемый узел не является корнем
{
int result = current.Parent.CompareTo(current.Value);
if (result > 0)
{
// Если значение родительского узла больше значения удаляемого,
// сделать левого потомка удаляемого узла, левым потомком родителя.
current.Parent.Left = current.Left;
}
else if (result < 0)
{
// Если значение родительского узла меньше чем удаляемого,
// сделать левого потомка удаляемого узла - правым потомком родительского узла.
current.Parent.Right = current.Left;
}
}
}
// Вариант 2: Если правый потомок удаляемого узла не имеет левого потомка, тогда правый потомок удаляемого узла
// становится потомком родительского узла.
else if (current.Right.Left == null) // если у правого потомка нет левого потомка
{
current.Right.Left = current.Left;
if (current.Parent == null) // текущий элемент является корнем
{
Head = current.Right;
if (Head != null)
{
Head.Parent = null;
}
}
else
{
int result = current.Parent.CompareTo(current.Value);
if (result > 0)
{
// Если значение узла родителя больше чем значение удаляемого узла,
// сделать правого потомка удаляемого узла, левым потомком его родителя.
current.Parent.Left = current.Right;
}
else if (result < 0)
{
// Если значение родительского узла меньше значения удаляемого,
// сделать правого потомка удаляемого узла - правым потомком родителя.
current.Parent.Right = current.Right;
}
}
}
// Вариант 3: Если правый потомок удаляемого узла имеет левого потомка,
// заместить удаляемый узел, крайним левым потомком правого потомка.
else
{
// Нахожление крайнего левого узла для правого потомка удаляемого узла.
AVLTreeNode<T> leftmost = current.Right.Left;
while (leftmost.Left != null)
{
leftmost = leftmost.Left;
}
// Родительское правое поддерево становится родительским левым поддеревом.
leftmost.Parent.Left = leftmost.Right;
// Присвоить крайнему левому узлу, ссылки на правого и левого потомка удаляемого узла.
leftmost.Left = current.Left;
leftmost.Right = current.Right;
if (current.Parent == null)
{
Head = leftmost;
if (Head != null)
{
Head.Parent = null;
}
}
else
{
int result = current.Parent.CompareTo(current.Value);
if (result > 0)
{
// Если значение родительского узла больше значения удаляемого,
// сделать крайнего левого потомка левым потомком родителя удаляемого узла.
current.Parent.Left = leftmost;
}
else if (result < 0)
{
// Если значение родительского узла, меньше чем значение удаляемого,
// сделать крайнего левого потомка, правым потомком родителя удаляемого узла.
current.Parent.Right = leftmost;
}
}
}
if (treeToBalance != null)
{
treeToBalance.Balance();
}
else
{
if (Head != null)
{
Head.Balance();
}
}
return true;
}
#endregion
#region Метод Clear
public void Clear()
{
Head = null; // удаление дерева
Count = 0;
}
#endregion
#region Итераторы
public IEnumerator<T> InOrderTraversal()
{
// рекурсивное перемищение по дереву
if (Head != null) // существует ли корень дерева
{
Stack<AVLTreeNode<T>> stack = new Stack<AVLTreeNode<T>>();
AVLTreeNode<T> current = Head;
// при рекурсивном перемещении по дереву, нужно указывать какой потомок будет слудеющим (правый или левый)
bool goLeftNext = true;
// Начинаем с помещения корня в стек
stack.Push(current);
while (stack.Count > 0)
{
// Если перемещаемся влево ...
if (goLeftNext)
{
// Перемещение всех левых потомков в стек.
while (current.Left != null)
{
stack.Push(current);
current = current.Left;
}
}
yield return current.Value;
// Если перемещаемся вправо
if (current.Right != null)
{
current = current.Right;
// Идинажды перемещаемся вправо, после чего опять идем влево.
goLeftNext = true;
}
else
{
// Если перейти вправо нельзя - извлекаем родительский узел.
current = stack.Pop();
goLeftNext = false;
}
}
}
}
public IEnumerator<T> GetEnumerator()
{
return InOrderTraversal();
}
System.Collections.IEnumerator System.Collections.IEnumerable.GetEnumerator()
{
return GetEnumerator();
}
#endregion
}
}
using System;
using System.Collections.Generic;
using System.Linq;
using System.Text;
using System.Threading.Tasks;
namespace AVLTreeNode
{
class Program
{
static void Main(string[] args)
{
AVLTree<int> Oak = new AVLTree<int>();
// 10 10
Oak.Add(10); // / \ / \
Oak.Add(3); // / \ / \
Oak.Add(2); // 3 12 ====> 3 15
Oak.Add(4); // / \ / \ / \ / \
Oak.Add(12); // 2 4 null 15 2 4 12 25
Oak.Add(15); // \
Oak.Add(11); // 25
Oak.Add(25); //
Oak.Remove(11);
foreach (var item in Oak)
{
Console.WriteLine(item);
}
Console.ReadKey();
}
}
}
